Oldal 23 [23]
(HT CHARISM A BI
Z ole.
TET
the RAW image conversion software." An encoding gamma of 1/2.2 (such as those using
SRGB and Adobe RGB 1998 colour) is commonly used (Figure 1-11(b)). In addition, S¬
shaped (tonal) curves may also be applied to the image if care is not taken to uncheck these
options (see Chapter 3). These processes redistribute native camera tonal levels into ones
closer to how the eye perceives them and add artistic enhancements, such as contrast and
saturation, to the images. In order to produce comparable images, the linear data describing
the tonal levels observed by the camera must be retrieved.
(a)
Recorded YV
INPUT:
Original Scene Luminance
0% 25% 50% 75% 100%
INPUT: Actual Luminance
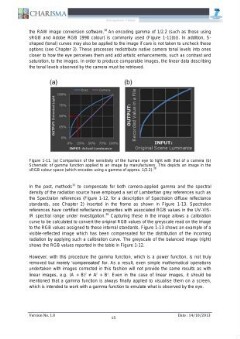
Figure 1-11. (a) Comparison of the sensitivity of the human eye to light with that of a camera (b)
Schematic of gamma function applied to an image by manufacturers. This depicts an image in the
sRGB colour space (which encodes using a gamma of approx. 1/2.2).*°
In the past, methods? to compensate for both camera-applied gamma and the spectral
density of the radiation source have employed a set of Lambertian grey references such as
the Spectralon references (Figure 1-12, for a description of Spectralon diffuse reflectance
standards, see Chapter 2) inserted in the frame as shown in Figure 1-13. Spectralon
references have certified reflectance properties with associated RGB values in the UV-VIS¬
IR spectral range under investigation.*? Capturing these in the image allows a calibration
curve to be calculated to convert the original RGB values of the greyscale read on the image
to the RGB values assigned to these internal standards. Figure 1-13 shows an example of a
visible-reflected image which has been compensated for the distribution of the incoming
radiation by applying such a calibration curve. The greyscale of the balanced image (right)
shows the RGB values reported in the table in Figure 1-12.
However, with this procedure the gamma function, which is a power function, is not truly
removed but merely ‘compensated’ for. As a result, even simple mathematical operations
undertaken with images corrected in this fashion will not provide the same results as with
linear images, e.g. (A + B)" # A” + B". Even in the case of linear images, it should be
mentioned that a gamma function is always finally applied to visualise them on a screen,
which is intended to work with a gamma function to emulate what is observed by the eye.
Version No. 1.0 15 Date : 14/10/2013